1. Variables and Relationships

First, let's look at a definition of a graph provided by some of the leading writers in Canadian introductory economics. Miller et al. define a graph as "a visual representation of the relationship between variables."¹ This definition emphasizes the importance of two aspects of graphs crucial to your understanding of what they do, which are variables and relationships.

A relationship is established in graphs between or among variables. Variables are quantities of data that change, and from which we want to establish trends. Variables are either independent or dependent. Variables and relationships in economics include the price of a good or service in relation to quantity demanded or supplied of a good or service, annual consumption expenditure in relation to annual real GDP, the Canadian interest rate in relation to annual planned expenditures of consumers, business, and government. We need to establish the differentiation between independent and dependent variables. For example, in social research, you may want to establish a relationship between height and weight. You could show that the weight of an individual is the dependent variable, dependent on the height of an individual, and height is an independent variable. More height is going to mean, ceteris paribus (other things being equal), greater weight. Less height is likely going to mean a lower weight. A dependent variable changes in relation to an independent variable, while an independent variable changes, for purposes of analysis, freely in value.

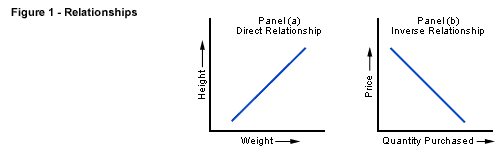
A relationship could be thought of as a connection; you connect two variables to establish an association. There are two relationships you need to know about in economics. A positive or direct relationship is one in which the two variables (we will generally call them x and y) move together, that is, they either increase or decrease together. An excellent example is the price of steel, and the response of steel suppliers to bring steel to the market; as the price increases, so does the willingness of producers to bring more of the good to the market. The example we gave of the relationship between height and weight is a direct or positive relationship.

In a negative or indirect relationship, the two variables move in opposite directions, that is, as one increases, the other decreases. Consider the price of coffee and the demand for the good. As the price of coffee, for example, goes to higher and higher levels, we can predict that people will substitute tea or hot chocolate for it, and buy less. As the price of coffee declines, people will buy more and more of it, and quite possibly buy more than they would regularly buy, and store or accumulate it for future consumption, or to sell it to others. This relationship is negative or indirect, that is, as the price variable (typically, in economics, the y variable) increases, the quantity variable (typically, the x variable) decreases; and, as the price variable decreases, the quantity demanded increases.

These relationships between positivly- and negatively-related variables are demonstrated in the graphs (Figure 1) which follow, positive first and negative second:

What is the value of graphs in the study of economics? Graphs are a very powerful visual representation of the relationship between or among variables. They assist learners in grasping fairly quickly key economic relationships. Years of statistical analysis have gone into the small graph you can examine to learn about key forces and trends in the economy. Further, they help your instructor to present data in a way which is small-scale or economical, and establish a relationship, frequently historical, between variables in a certain kind of relationship. They permit learners and instructors to establish quickly the peaks and valleys in data, to establish a trend line, and to discuss the impact of historical events such as policies on the data that we wish to analyze.

2. Types of Graphs in Economics

There are various kinds of graphs used in business and economics that illustrate data. These include pie charts (segments are displayed as portions, usually percentages, of a circle), scatter diagrams (points are connected to establish a trend), bar graphs (results for each year can be displayed as an upward or downward bar), and cross section graphs (segments of data can be displayed horizontally). You will deal with some of these in economics, but you will be dealing principally with graphs of the following variety.

Certain graphs display data on one variable over a certain period of time. For example, we may want to know how the inflation rate has varied in the Canadian economy from 1990-1999. We would choose an appropriate scale for the rate of inflation on the y (vertical) axis; and on the x (horizontal) axis show the ten years from 1990 to 1999 with 1990 on the left, and 1999 on the right. We could show the inflation rate or percentage changes to the Consumer Price Index (CPI) as a curve or line. We would notice right away a trend. The trend in the inflation rate data is a decline, actually from a high of 5.6% in 1991 to a low of 0.2% in 1994. We would see that there has been some increase in the inflation rate since its absolute low in 1994, but not anything like the 1991 high. And, if we did such graphs for each of the decades in Canada since 1960, we would see that the 1990s were a unique decade in terms of inflation. No decade, except the 1960s, shows any resemblance to the 1990s. We can then discuss the trends meaningfully, since we have ideas about the data over a major period of time. We can link the data with historical events such as government anti-inflation policies, and try to establish some connections.

Other graphs are used to present a relationship between two variables, or in some instances, among more than two variables. Consider the relationship between price of a good or service and quantity demanded. The two variables move in opposite directions, and therefore demonstrate a negative or indirect relationship. Aggregate demand, the relationship between the total quantity of goods and services demanded in the entire economy, and the price level, also exhibits this inverse or negative relationship. If the price level (based on the prices of a given base year) rises, real GDP shrinks; while if the price level falls, real GDP increases.

Further, the supply curve for many goods and services exhibits a positive or direct relationship. The supply curve shows that when prices are high, producers or service providers are prepared to provide more goods or services to the market; and when prices are low, service providers and producers are interested in providing fewer goods or services to the market. The aggregate expenditure, or supply, curve for the entire Canadian economy (the sum of consumption, investment, government expenditure and the calculation of exports minus imports) also shows this positive or direct relationship. Aggregate planned expenditure increases as real GDP increases, and decreases as real GDP diminishes.

3. Construction of a Graph

You will at times be asked to construct a graph, most likely on tests and exams. You should always give close attention to creating an origin, the point 0, at which the axes start. Label the axes or number lines properly, so that the reader knows what you are trying to measure. Most of the graphs used in economics have, a horizontal number line or x-axis, with negative numbers on the left of the point of origin or 0, and positive numbers on the right of the origin. Figure 2 presents a typical horizontal number line or x-axis.

In economics graphs, you will also find a vertical number line or y-axis. Here numbers above the point of origin (0) will have a positive value; while numbers below 0 will have a negative value. Figure 3 demonstrates a typical vertical number line or y-axis.

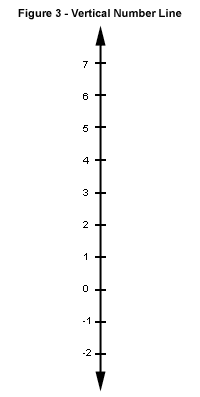
When constructing a graph, be careful in developing your scale, the difference between the numbers on the axes, and the relative numbers on each axis. The scale needs to be graduated or drawn properly on both axes, meaning that the distance between units has to be identical on both, though the numbers represented on the lines may vary. You may want to use single digits, for example, on the y-axis, while using hundreds of billions on the x-axis. Using a misleading scale by squeezing or stretching the scale unfairly, rather than creating identical distances for spaces along the axes, and using a successive series of numbers will create an erroneous impression of relationship for your reader.

If you are asked to construct graphs, and to show a knowledge of graphing by choosing variables yourself, choose carefully what you decide to study. Here is a good example of a difficulty to avoid. Could you, for example, show a graphical relationship between good looks and high intelligence? I don't think so. First of all, you would have a tough time quantifying good looks (though some social science researchers have tried!). Intelligence is even harder to quantify, especially given the possible cultural bias to most of our exams and tests. Finally, I doubt if you could ever find a connection between the two variables; there may not be any. Choose variables that are quantifiable. Height and weight, caloric intake and weight, weight and blood pressure, are excellent personal examples. The supply and demand for oil in Canada, the Canadian interest rate and planned aggregate expenditure, and the Canadian inflation rate during the past forty years are all quantifiable economic variables.

You also need to understand how to plot sets of coordinate points on the plane of the graph in order to show relationships between two variables. One set of coordinates specify a point on the plane of a graph which is the space above the x-axis, and to the right of the y-axis. For example, when we put together the x and y axes with a common origin, we have a series of x,y values for any set of data which can be plotted by a line which connects the coordinate points (all the x,y points) on the plane.

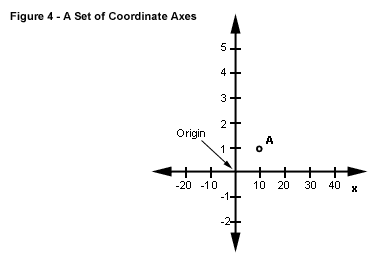
Figure 4 below shows an x- and y-axis, an origin, and a paired observation of the variables, a coordinate point on the plane of the graph at x = 10, and y = 1. Such a point can be expressed inside brackets with x first and y second, or (10,1). A set of such paired observation points on a line or curve which slopes from the lower left of the plane to the upper right would be a positive, direct relationship. A set of paired observation or coordinate points on a line that slopes from the upper left of the plane to the lower right is a negative or indirect relationship.

4. Working from a Table to a Graph

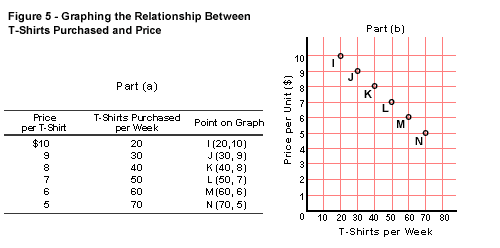
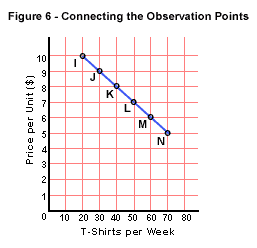
Figures 5 and 6 present us with a table, or a list of related numbers, for two variables, the price of a T-shirt, and the quantity purchased per week in a store. Note the series of paired observation points I through N, which specify the quantity demanded (x-axis, reflecting the second column of data) in relation to the price (y-axis, reflecting first column of data). See that by plotting each of the paired observation points I through N, and then connecting them with a line or curve, we have a downward sloping line from upper left of the plane to the lower right, a negative or inverse relationship. We have now illustrated that as price declines, the number of T-shirts demanded or sought increases. Or, we could say reading from the bottom, as the price of T-shirts increases, the quantity demanded decreases. We have stated here, and illustrated graphically, the Law of Demand in economics.

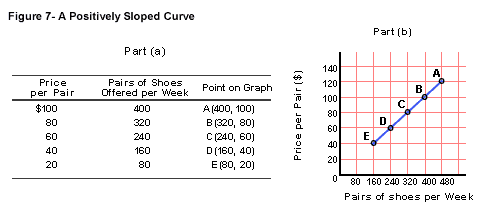
Now we can turn to the Law of Supply. The positive relationship of supply is aptly illustrated in the table and graph of Figure 7. Note from the first two columns of the table that as the price of shoes increases, shoe producers are prepared to provide more and more goods to this market. The converse also applies, as the price that consumers are willing to pay for a pair of shoes declines, the less interested are shoe producers in providing shoes to this market. The x,y points are specified as A through to E. When the five points are transferred to the graph, we have a curve that slopes from the lower left of the plane to the upper right. We have illustrated that supply involves a positive relationship between price and quantity supplied, and we have elaborated the Law of Supply.

Now, you should have a good grasp of the fundamental graphing operations necessary to understand the basics of microeconomics, and certain topics in macroeconomics. Many other macroeconomics variables can be expressed in graph form such as the price level and real GDP demanded, average wage rates and real GDP, inflation rates and real GDP, and the price of oil and the demand for, or supply of, the product. Don't worry if at first you don't understand a graph when you look at it in your text; some involve more complicated relationships. You will understand a relationship more fully when you study the tabular data that often accompanies the graph (as shown in Figures 5 and 7), or the material in which the author elaborates on the variables and relationships being studied.

5. Steep vs. Gentle Slopes

When you have been out running or jogging, have you ever tried, at your starting pace, to run up a steep hill? If so, you will have a good intuitive grasp of the meaning of a slope of a line. You probably noticed your lungs starting to work much harder to provide you with extra oxygen for the blood. If you stopped to take your pulse, you would have found that your heart is pumping blood far faster through the body, probably at least twice as fast as your regular, resting rate. The greater the steepness of the slope, the greater the sensitivity and reaction of your body's heart and lungs to the extra work.

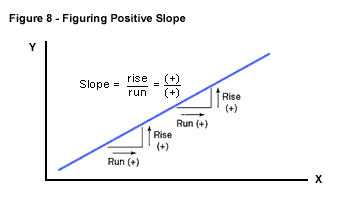
Slope has a lot to do with the sensitivity of variables to each other, since slope measures the response of one variable when there is a change in the other. The slope of a line is measured by units of rise on the vertical y-axis over units of run on the horizontal x-axis. A typical slope calculation is needed if you want to measure the reaction of consumers or producers to a change in the price of a product.

For example, let's look at what happens in Figure 7 when we move from points E to D, and then from points B to A. The rise or vertical movement from E to D is 20, calculated by 40 - 20 = 20. The run or horizontal movement is 80, calculated from the difference between 160 and 80, which is 80. The slope = run / rise is therefore, 20 / 80, which is ¼, or 0.25. Let's look at the change between B and A. The vertical difference is again 20 (100 - 80), while the horizontal difference is 80 (400 - 320). So, the slope is, again, ¼, or 0.25. We can generalize to say that where the curve is a straight line, the slope will be a constant at all points on the curve. Figure 8 shows that where right-angled triangles are drawn to the curve, the slopes are all constant, and positive.

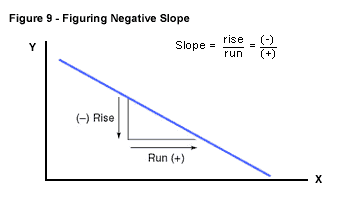
Now, let's take a look at Figure 9, which shows the curve of a negative relationship. All slopes in a negative relationship have a negative value. If we look, for example, at the change between points I and J in Figure 6, we find a -1 rise (9 - 10 = -1), and a +10 run (30 - 20 = 10). The slope on this negative relationship curve is, therefore, -1/10 or -0.1. We can generalize to say that for negative relationships, increases in one variable are associated with decreases in the other, and slope calculations will, therefore, be of a negative value.

A final word on non-linear slopes. Not all positive nor negative curves are straight lines, and some curves are parabolic, that is, they take the shape of a U or an inverted U, as is demonstrated in Figure 10, shown below. To the left of point C, called the maxima, slopes are positive, and, to the right of point C, they are negative. You can determine the slope of a parabola by drawing a tangent (touches at a single point) line to any point on the curve. You can see below that a point such as R is then selected on the line, and a right angled triangle can be constructed which joins points R and B. We can then calculate the rise over the run between points B and R from the distance of the height and the base of the triangle. So, we can generalize to say that the slopes of a non-linear line are not constant like a straight line and will vary in sign and in value.

You will find that a knowledge of slope calculations enhances your understanding of the dynamics of graphs. It will likely improve your marks in economics, since many test questions require you to illustrate your thinking with graphs.

Summary

A person from an Eastern culture once observed, "A picture is worth a thousand words." So are graphs. Without them, we would be forced to examine thousands, or tens of thousands, of bits of statistical information to determine economic relationships. Many economic researchers over the years have done that work for you, and it gets expressed in nice little packages called graphs. They convey information easily, efficiently, and effectively, and can stimulate good thought and discussion.

Notes
1. R. L. Miller, B. Abbott, S. Fefferman, R. K. Kessler, and T. Sulyma, Economics Today: The Micro View, Second Canadian Edition. (Toronto: Pearson Education Canada, 2002), p. 40.